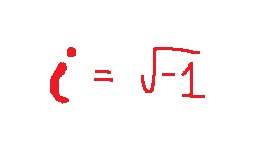jueves, 11 de agosto de 2011
Recopilación de Números complejos
No es tan complejo, es cosa de leer un poco y hacer unos cuantos ejercicios
1._ ¿Qué son?
2._ Suma, resta y sus propiedades
3._ Multiplicación, división y propiedades
4._ Su mística geometría ¿Te recuerdan a algo?
5._ Forma polar
6._ Potencias y raíces
7._ Ejercicios
Descarga el libro, esta todo esto y mucho más (muy recomendado)
Una Introducción a los Números Complejos; por Francisco Rivero Mendoza
Números complejos: Segunda parte parte Suma, resta y sus propiedades
Suma de complejos
La suma de números complejos esta basada en la suma de números reales. Para sumarlos hay que sumar las partes reales por un lado y la parte imaginaria por otro lado, como números reales:
Ejemplo: si sumamos Z1 y Z2
Resta de complejos
La diferencia de complejos se realiza restando cada parte por separado.
Ejemplo: si restamos Z1 y Z2
Propiedades de suma y resta
Próximo capitulo multiplicación y división.
La suma de números complejos esta basada en la suma de números reales. Para sumarlos hay que sumar las partes reales por un lado y la parte imaginaria por otro lado, como números reales:
Ejemplo: si sumamos Z1 y Z2
Resta de complejos
La diferencia de complejos se realiza restando cada parte por separado.
Ejemplo: si restamos Z1 y Z2
Propiedades de suma y resta
Próximo capitulo multiplicación y división.
miércoles, 10 de agosto de 2011
Números complejos: primera parte ¿Qué son?
Un número complejo es una expresión de tipo
a y b son números reales
"i", es el símbolo imaginario.
Z es el número complejo.
Por lo que podemos decir que estos números posen una parte real y una parte imaginaria.
¿De donde viene el símbolo "i"?
Todo surge de ecuaciones que no tienen soluciones comunes, como por ejemplo:
a y b son números reales
"i", es el símbolo imaginario.
Z es el número complejo.
Por lo que podemos decir que estos números posen una parte real y una parte imaginaria.
¿De donde viene el símbolo "i"?
Todo surge de ecuaciones que no tienen soluciones comunes, como por ejemplo:
Para encontrar las soluciones de X ocupamos la formula:
Entonces para resolver la anterior ecuación nos daría algo como:
Fijémonos bien en la siguiente expresión:
¿Qué pasa con raíz negativa de tres? Está expresión no tiene sentido en los números reales, osea los que habituamos usar en nuestra peculiar realidad.
Ya que, si existiese raíz de menos tres, quiere decir que un número multiplicado por sí mismo de la forma (x**2), da como resultado un número negativo. Ya sabemos que :
Entonces se dice que:
Entonces se acepta el símbolo raíz de menos uno como una entidad matemática nueva:
Por lo tanto la ecuación que no tenía solución nos queda:
muy importante saber que:
Las expresiones Re(z), Im(z) se ocupan harto en ejercicios, como por ejemplo para sacar solo la parte imaginaria o solo la real.
Ejemplo:
El siguiente es un número complejo:
Donde 5 es la parte real y 8 es la parte imaginaria.
Próximo cápitulo: sumas y restas.
domingo, 7 de agosto de 2011
Logaritmos (incompleta aún)
¿Qué es un Logaritmo?
Un logaritmo solo es una forma de ordenar un numero exponencial. Es decir:
En logaritmo esto se escribiría así:
Ejemplo:
2._
Ejemplo:
3._
Hacer los siguientes ejercicios:
Más ejercicios resueltos:
¿Cómo calcular el logaritmo de un número cuando te dan de referencia otro?
Un logaritmo solo es una forma de ordenar un numero exponencial. Es decir:
En logaritmo esto se escribiría así:
-Osea, el número pequeño es la base, en este caso el 3
-El numero grande que va después, es el resultado llamado Argumento
-el resultado del logaritmo sería a que número tiene que estar elevado 3, para que nos de como resultado 9
¿Porque se hace esto?
Por ejemplo nosotros tenemos duda en el siguiente ejercicio:
¿cinco elevado a que número me da 125?
El logaritmo nos ayuda a escribirlo así:
"OSEA ES SOLO UNA MANERA DIFERENTE DE ESCRIBIR UN NUMERO ELEVADO"
Está claro que el resultado del ejercicio anterior es 3. pero existen algunos logaritmos más complejos como:
Aquí decimos ¿ ocho elevado a que número me da 30 ?, no existe ningún número entero para definir ese ejercicio, solo podríamos saberlo por calculadora.
Es por eso que existen ciertas propiedades, para sumar, restar, una serie de logaritmos, asi llegar a un resultado más coherente.
Propiedades:
Explicaremos uno por una estas propiedades:
1._
Cuando tenemos un logaritmo que tiene cualquier base, por eso se expresa con el número a, y tiene con argumento el número uno, siempre va a dar como resultado cero. Esto pasa porque cualquier número elevado a cero, es uno:
Ejemplo:
2._
todo logaritmo, que tenga una base igual a su argumento, siempre dará uno como resultado.
¿Porque?
Porque todo numero elevado a uno, siempre va a dar resultado el mismo número.
Ejemplo:
3._
Siempre que el argumento este elevado a un numero uno puede hacer lo siguiente:
Lo movemos a un principio así desarrollar el ejercicio sin él
ejemplo:
Más ejercicios resueltos:
¿Cómo calcular el logaritmo de un número cuando te dan de referencia otro?
¿Qué son lo logaritmos en base 10?
Es muy sencillo, como el nombre lo dice es cuando la base de ellos es 10.
Lo que tienen de especial es que no se escribe la base del logaritmo, por lo tanto solo se anota:
Ahora seguiremos con las otras propiedades:
4._
Esta propiedad es muy importante, la suma de logaritmos SOLO QUE TIENEN IGUAL BASE, se pueden multiplicar sus argumentos o al revés. La resta de logaritmos SOLO QUE TIENE IGUAL BASE, se pueden dividir sus argumentos.
Ejemplos:
Suscribirse a:
Comentarios (Atom)